確率・統計の教科書を参照してください 確率変数random variable •重要な公式 Var( )=E 2)− 2 •連続型変数の期待値、分散も離散型の自然な拡張 です→確率・統計の教科書を参照 同時分布(離散分布の場合) 確率変数XとYに対し •同時確率(joint probability) ( , )≡Pr = , = •周辺確率(marginal確率変数:取る値の範囲と取る確率だけがわかっている「変数」 1 確率変数の種類 分散公式 V(X) = E(X2) 2 証明 離散確率変数の場合に証明しておく. V(X) = E((X )2) = E(X2 2 X 2) = ∑ i (x2 i 2 xi 2)p(x i) = ∑ i x2 i p(xi) 2 ∑ i xip(xi) 2 ∑ i p(xi) = E(X2) 2 E(X) 2 = E(X2) 2 上で ∑ i p(xi) = 1 とE(X) = であることを確率の公式 では確率の公式について見ていきましょう。 確率の公式 全部でn n 通りの事柄が起こる可能性があり、どれも同様に確からしいとする。 そのうち、事柄A A の起こる場合がa a 通りで、その確率をp p とすると、 p = a n p = a n 0 ≦p ≦1 0 ≦ p ≦ 1 ※同様に確からしい:どれも同じ起こりやすさ(同じ確率) 『0 ≦p ≦1 0 ≦ p ≦ 1 』というのは、確率は0以上1
確率とは 公式 問題での計算式の立て方と解き方 受験辞典
確率 公式 使い分け
確率 公式 使い分け-˘ p 2ˇnnne n 証明 logn!確率分布公式集 清水邦夫、渋谷政昭、横内大介、高際睦* 慶応義塾大学理工学部(* 東京歯科大学)




反復試行の確率 なぜこんな公式になるの Cを使う理由は 数スタ
= n(n−1)(n−2)···(n−r 1) r(r −1)(r −2)···2 ·1 = n!どのような確率モデルと母数推定法を仮定したかには依存しない理論cdfである。したがって、式 (31)ははじめに仮定した各地点の年最大値確率モデルF( )の既往最大値付近の分布適合度検定 のための客観的指標となる11)。 4プロッティング・ポジション公式 まとめ:確率の求め方の公式・計算式は1つで十分 中学で勉強する確率の公式は1つ。 P (A) = (ことがらAが起きる場合の数)÷(すべての場合の数)
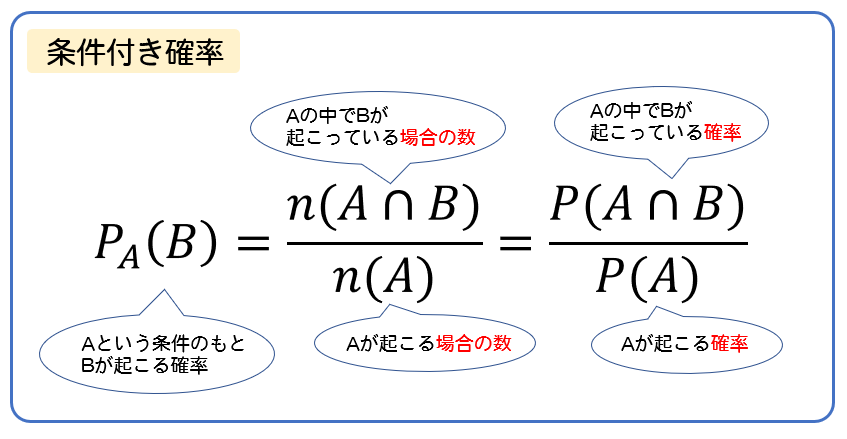
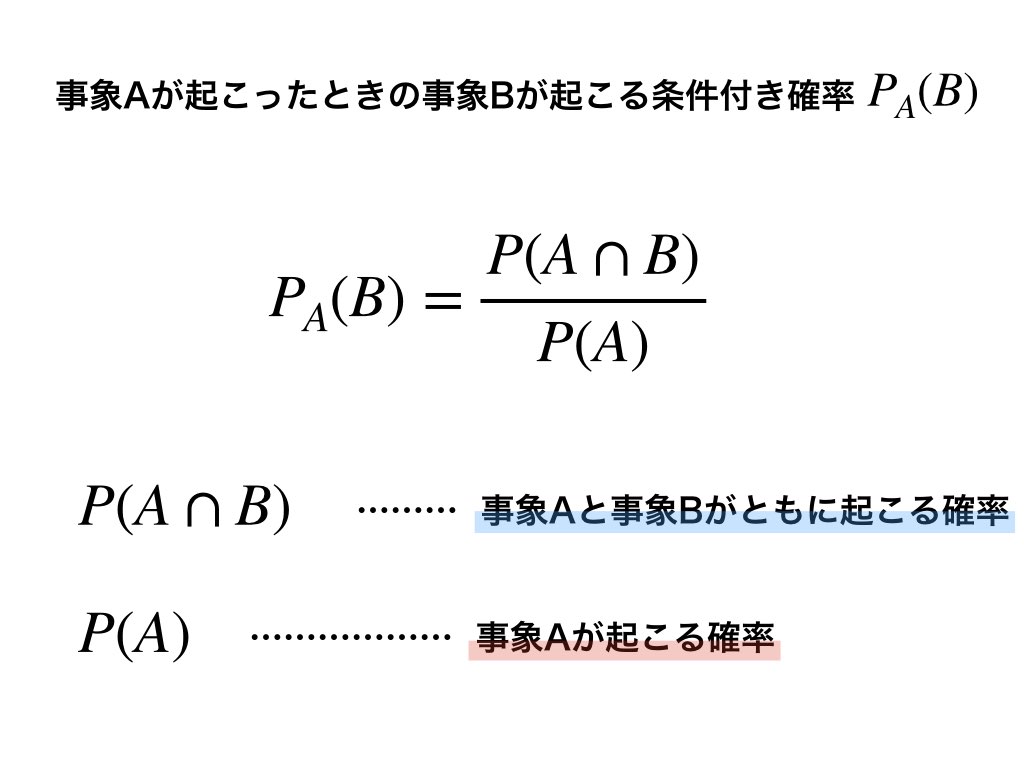
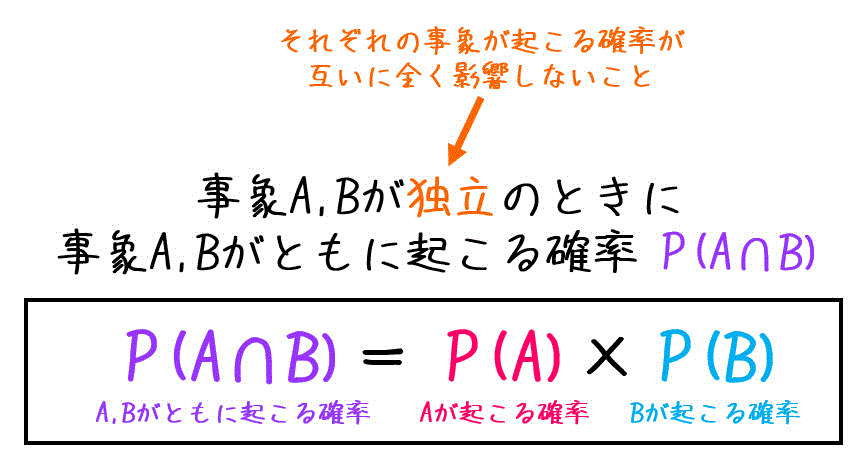
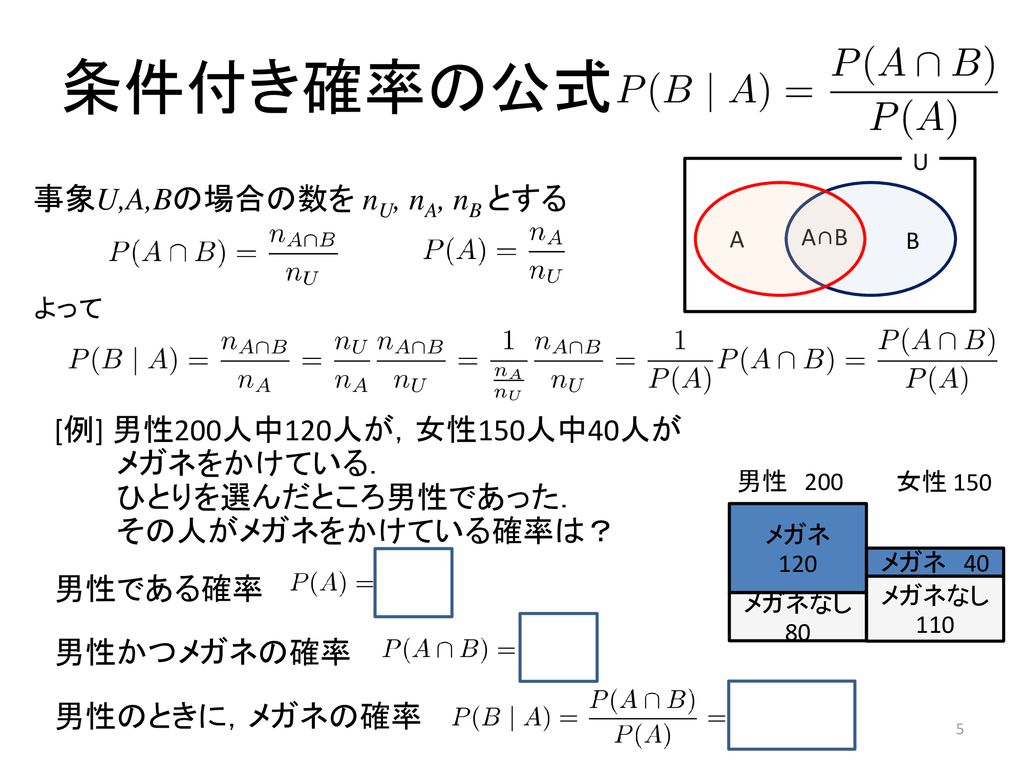
確率積分と確率微分方程式 Stochastic Integrals and Stochastic fftial Equations 重要な道具である確率積分(伊藤積分)や伊藤の公式 等について解説し, 基本となるマルコフ過程について, 確率微分方程式を用いて, どんな性質をどの ように調べるか, ということについてその一端を紹介したいと思うただし、nC0 =1 A13 nC r の基本性質 nC r = nC n−r nC r = n−1C r−1 事象aが起きるときに事象bも起きる条件付き確率\(p_{a}(b)\)は以下の公式で求めます。 条件付き確率 \(\displaystyle P_{A}(B)=\frac{P(A \cap B)}{P(A)}\)
公式集:数理統計学 A 確率 A—1 確率 A11 異なるn 個のものからr 個とる順列 nP r = n(n−1)(n−2)···(n−r 1) A12 異なるn 個のものからr とる組み合わせ nC r = nP r r!確率論II 種村秀紀 千葉大学理学部数学・情報数理学科 つぎにスターリングの公式をしめす この公式を最初に発見したのは, ド・モアブルであるが, スターリ ングの貢献は, 定数が p 2ˇ であることを決定したことである 補題12 (スターリングの公式) (15) n!順列、組み合わせ、二項定理 数学についてのwebノート ・定義: 順列 ・ 組み合せ ・定理: 組合せの性質 ・ 二項定理 ・ 多項定理 ※ 総目次




ベイズの定理とは何か 条件付き確率からわかる判別の知恵 アタリマエ




確率がわかりません カッコ1だけでもいいので教えていただきたいです お願いします Clear
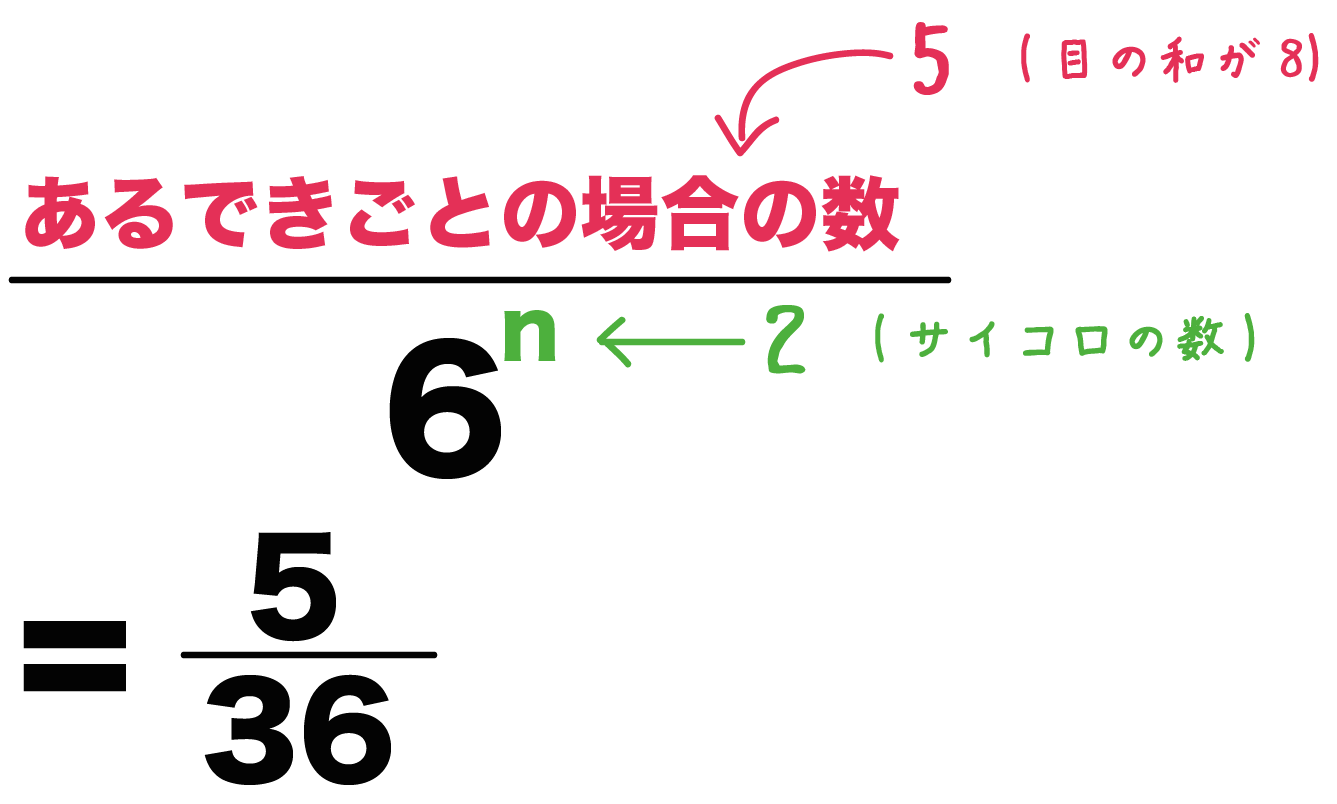
と書けるので、全確率の公式は次のようにも書けます。 \ \begin{aligned} P(A) &= \sum^n_{k=1} P(A S_k) P(S_k) \end{aligned} \ それでは、この式を使う問題を考えてみましょう。 たった一つの公式を使って求めることができる中学の確率 中学校2年で習う確率の公式は、たったの一つです。 確率は、 $$\text{確率} = \frac{\text{ある条件が起こる場合の数}}{\text{すべての場合の数}}$$ で計算できます。 これだけです。 どんな確率の問題もこの公式さえ使うことができれば解けてしまいます。 公式の分子と分母には、"場合の数"が入りますね 公式は内容を考えると当たり前ですかね。 ここまでの公式をまとめておきます。どうやって作られたかも必ずみてくださいね。 確率の和と積の違い 独立試行とは こんにちは。 da Vinch (@mathsouko_vinch)です。 確率とは 確率はもともとカジノや賭け事を有利に進める、もしくは最終




反復試行の確率 なぜこんな公式になるの Cを使う理由は 数スタ



統計学 期待値 分散の公式 離散型と連続型における公式をわかりやすく証明 脱仙人からの昇天 からのぶろぐ
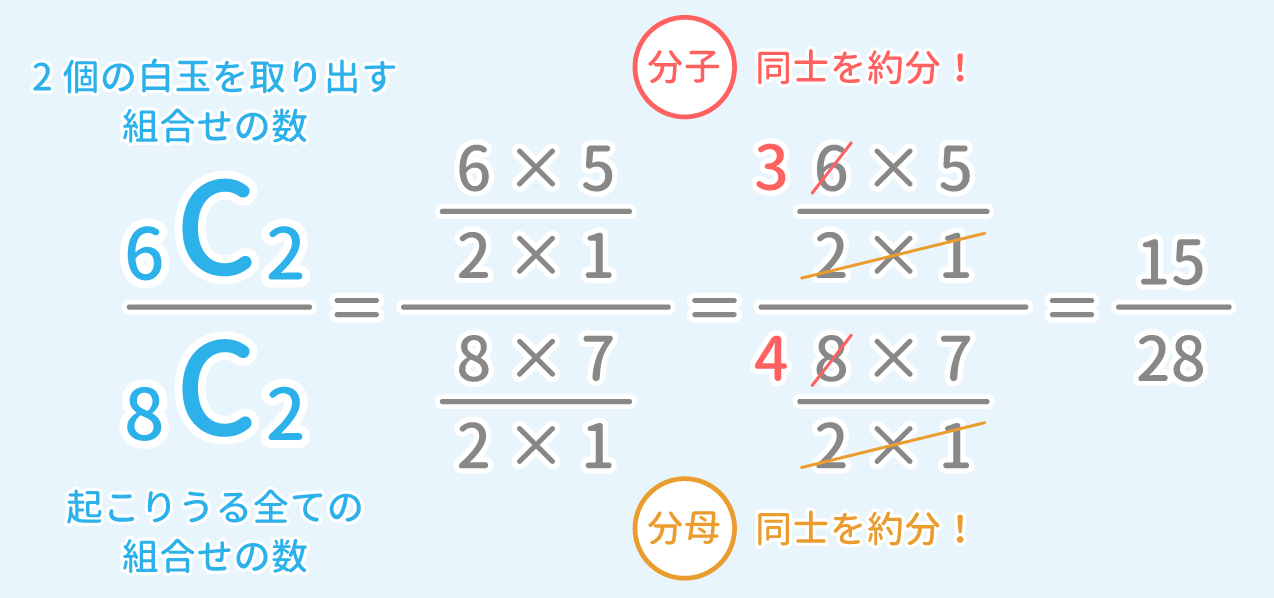
円順列 公式とその考え方 こんにちは。 da Vinch ( @mathsouko_vinch )です。 Contents 円順列と通常の順列の違い 円順列の考え方1 数えすぎを割る 円順列の考え方2 1つ固定して順列で 円順列の公式 まとめ確率の計算を行う場合、場合の数で学んだ組み合わせ(c)や順列(p)、あるいは集合 の考え方を用いることでより効率よく計算できます。 例題: 白いボール3個と赤いボール7個があります。この中から無作為にボールを3つ取り出すとき、次のような事象が起こる確率はいくらでしょうか。 条件付き確率の公式 さて,ここで一度具体例から離れて,次の「条件付き確率」を求める公式を導出します. 公式とその導出 まず記号ですが,事象Sが起こる場合の数を$n(\mrm{S})$,事象$S$が起こる確率を$P(\mrm{S})$と書きます.



Spi M54e217p7lcis9d Com Category E7 Ba E7 8e 87



確率とは 公式 問題での計算式の立て方と解き方 受験辞典
を用いて計算すればよい。 (I) 5 C 2 = 5 × 4 2 × 1 = 10 {\displaystyle {}_ {5}C_ {2}= {\frac {5\times 4} {2\times 1}}=10} (II) 7 C 3 = 7 × 6 × 5 3 × 2 × 1 = 35 {\displaystyle {}_ {7}C_ {3}= {\frac {7\times 6\times 5} {3\times 2\times 1}}=35} (III) 10 C 1 = 10 1 = 10確率とは、事象の確からしさを表わす尺度で、0 以上1 以下の値を取り、必ず起こる事象の確率 は1, 起こらない事象の確率は0, などの性質を持っている。期待値と分散の公式 期待値 定義 和の期待値 定数倍の期待値 定数を加えた期待値 期待値の一般的性質 分散 定義 和の分散 定数倍の分散 定数を加えた分散 分散の一般的性質 関係・性質 分散と期待値および二乗期待値の関係 独立な確率変数の積の期待値 独立な確率変数の
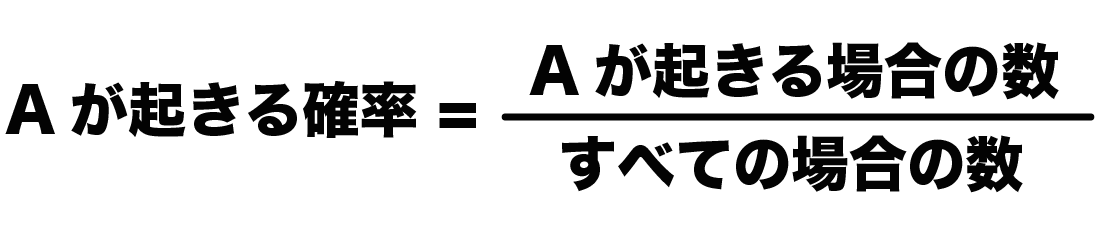



中学数学 確率の求め方がわかる1つの公式 計算式 Qikeru 学びを楽しくわかりやすく




中学2年数学 確率 確率の求め方 たった1つの公式ですべてわかる 数学の面白いこと 役に立つことをまとめたサイト
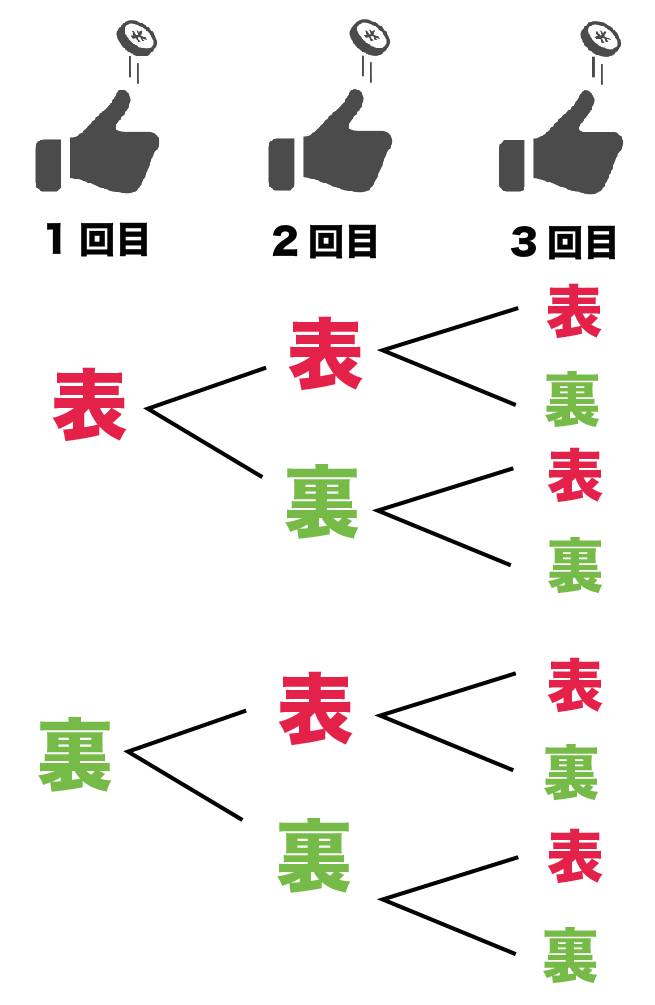
Aの起こる確率 は次のように表せます。 ②確率を求めるにあたって、場合の数を数えるとき、抜けが無いようにするため、組合せで考えて場合を書き出し(昇順または降順で書き出す)、順列の計算を行います。 ③確率を計算するときは、同じものも全て区別する必要があります 例 Aが3つある場合にはA1,,A3のように分けます。 (1) 3つのさいころを同時に投げる 数学Aの教科書に載っている公式の解説一覧 まとめ 更新日時 数Aの教科書(新課程)に載っている公式(や定義など)を整理しました。 新課程では三分野から二分野選んで学習するシステム になっていますが,(多くの大学で)入試を突破するに 確率とは?公式 確率とは、 ある事象(出来事)の起こりやすさ(割合) のことです。 確率は、英単語「Probability」の頭文字をとって、記号 \(P\) で表します。




確率統計 Ncrとnpr Dinop Com



中学数学 確率の求め方がわかる1つの公式 計算式 Qikeru 学びを楽しくわかりやすく
解答 反復試行の確率の公式で n = 4, k = 2, p = 1 6 n=4,k=2,p=\dfrac {1} {6} n = 4,k = 2,p = 61 の場合なので, 4 C 2 ( 1 6) 2 ( 5 6) 2 = 25 216 {}_4\mathrm {C}_2\left (\dfrac {1} {6}\right)^2\left (\dfrac {5} {6}\right)^2=\dfrac {25} {216} 4漸近公式 分布収束(6/12) 定理53 確率変数列X1,X2,がX に確率収束すれば, その確率変数列は X に分布収束している すなわち →p X ⇒ X n →d X が成り立つ とくに, X ∼ U(c)のときは, 逆も成り立つ した がって →d c ⇔ X n →p c が成り立つ 条件付き確率の公式の説明 条件付き確率については、ベン図を用いると直感的に理解できるかと思います。 条件付き確率の式、 は、その式の形から、 に対する の比を意味しており、それは上図における赤色部分に対する黄色部分の比になります。
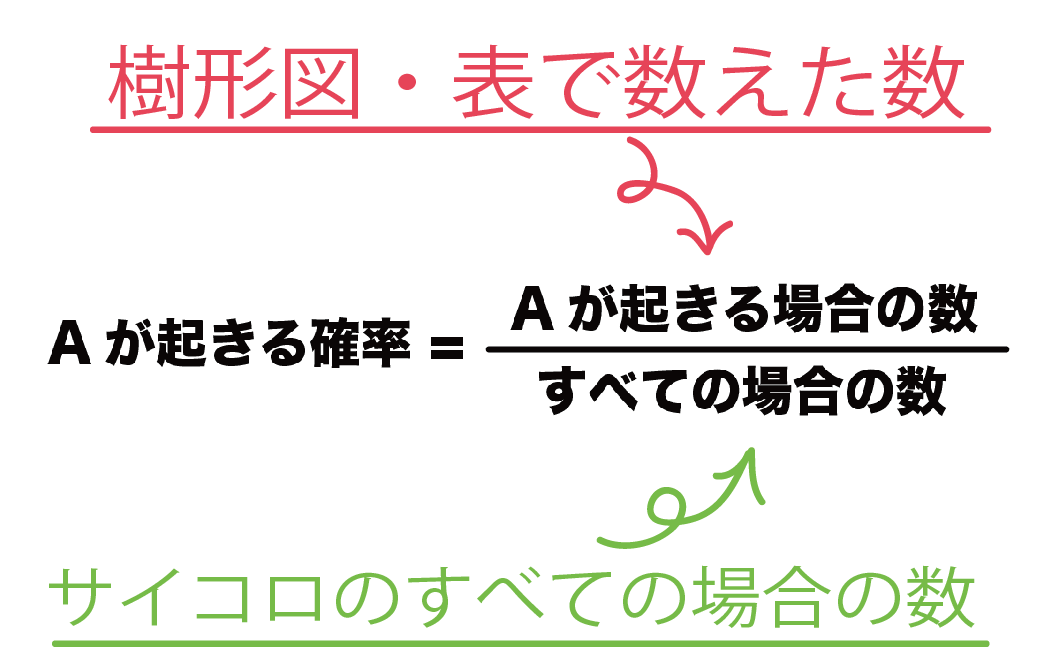



中2数学 サイコロの目の確率を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




確率9 反復試行の公式はない方がよい 怜悧玲瓏 高校数学を天空から俯瞰する
多変数の確率分布 L01条件付き確率の性質2'の誤記訂正 性質2'(周辺確率との関係) fX(xi) = ∑ j fXjY(xijyj)fY(yj) fY(yj) = ∑ i fYjX(yjjxi)fX(xi) 導出 同時確率の式を加えて周辺確率を出した 樋口さぶろお(数理情報学科) L02 確率変数の独立性・ベイズの公式 確率統計☆演習II(16) 2 / 23




条件付き確率




条件付き確率とは 公式を使ってサイコロ 玉の問題を解いてみよう くじ引きを用いた例題付き 高校生向け受験応援メディア 受験のミカタ




公式や解法が使えない 思い付かない時の対処法教えます




条件付き確率 の公式が感覚的に理解できる解説 練習問題 数学fun
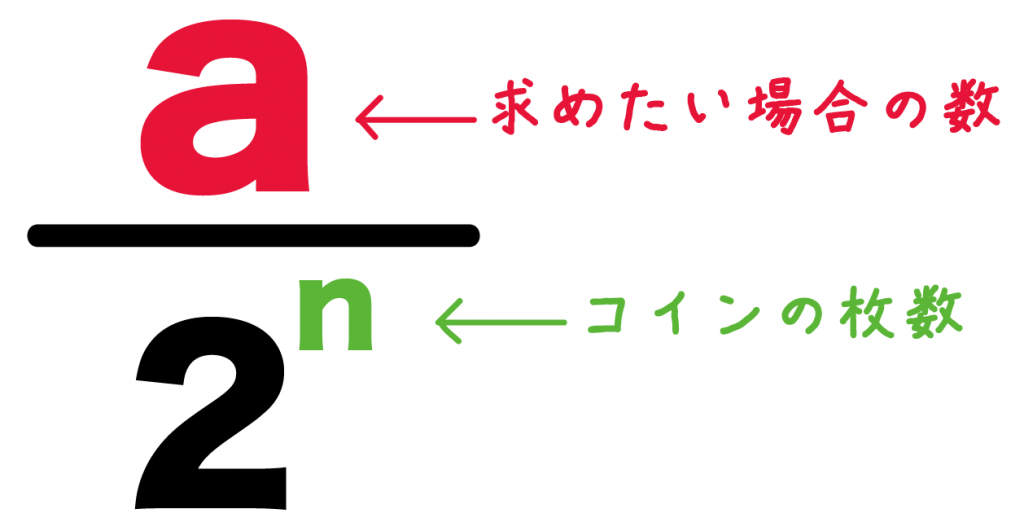



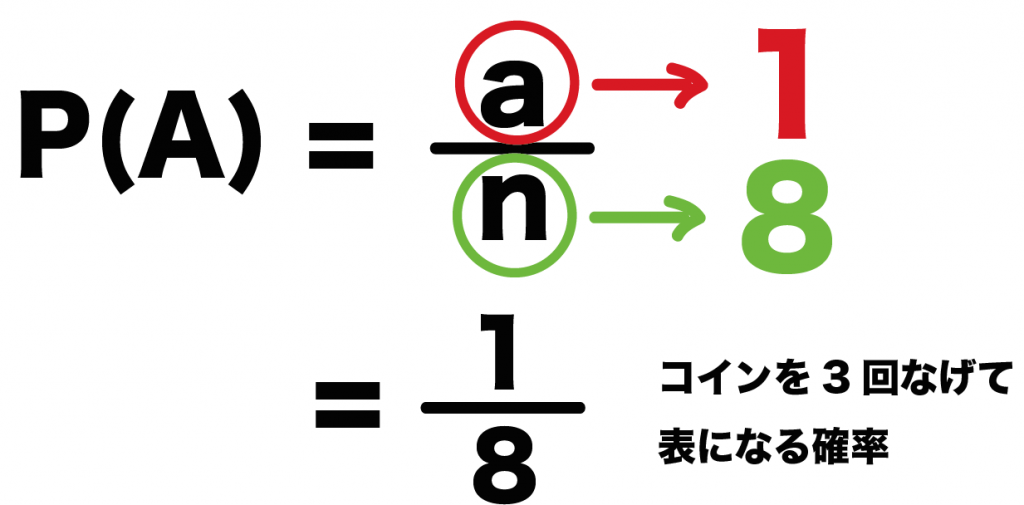
簡単公式 コインの確率を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく




確率 反復試行の確率の公式とその例題 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




反復試行の確率とは 公式の意味をしっかりと理解する 高校数学の知識庫




確率 条件つき確率について 日々是鍛錬 ひびこれたんれん




中学数学 確率 確率の求め方 たった1つの公式ですべてわかる Youtube



苦手な人向け 条件付き確率の考え方を図を使ってイチからわかりやすく 数スタ



中学数学 確率の求め方がわかる1つの公式 計算式 Qikeru 学びを楽しくわかりやすく




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ




場合の数と確率 の記事一覧
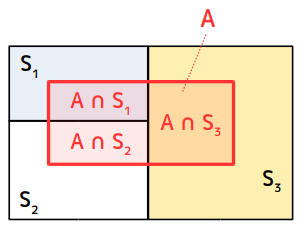



全確率の公式 確率統計 基礎からの数学入門




高校数学a 反復試行の確率 先にk回起こる 受験の月




じゃんけんの確率の解き方を教えてください Clear




反復試行の確率の求め方 数学の偏差値を上げて合格を目指す



確率とは 公式 問題での計算式の立て方と解き方 受験辞典



Spi 確率 最速解法 例題 Study Pro Spi



中2数学 サイコロの目の確率を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




条件付き確率 数学の偏差値を上げて合格を目指す




確率 怜悧玲瓏 高校数学を天空から俯瞰する




確率10 反復試行の公式はない方がよい2 怜悧玲瓏 高校数学を天空から俯瞰する




確率分布 の公式集 高校数学なんちな



場合の数と確率を総まとめ 各種公式 重要記事一覧 受験辞典



確率 1時間でマスター 覚えておくべき5つの法則 公式 工業大学生ももやまのうさぎ塾




大学数学 確率統計入門13 全確率の公式 ベイズの定理 Youtube



確率の公式と基本的な問題の解き方 数学fun



2



条件付き確率 わからないなら このやり方でやってみよう 家庭教師の想い




数学の公式 定理集 場合の数と確率 日々是鍛錬 ひびこれたんれん
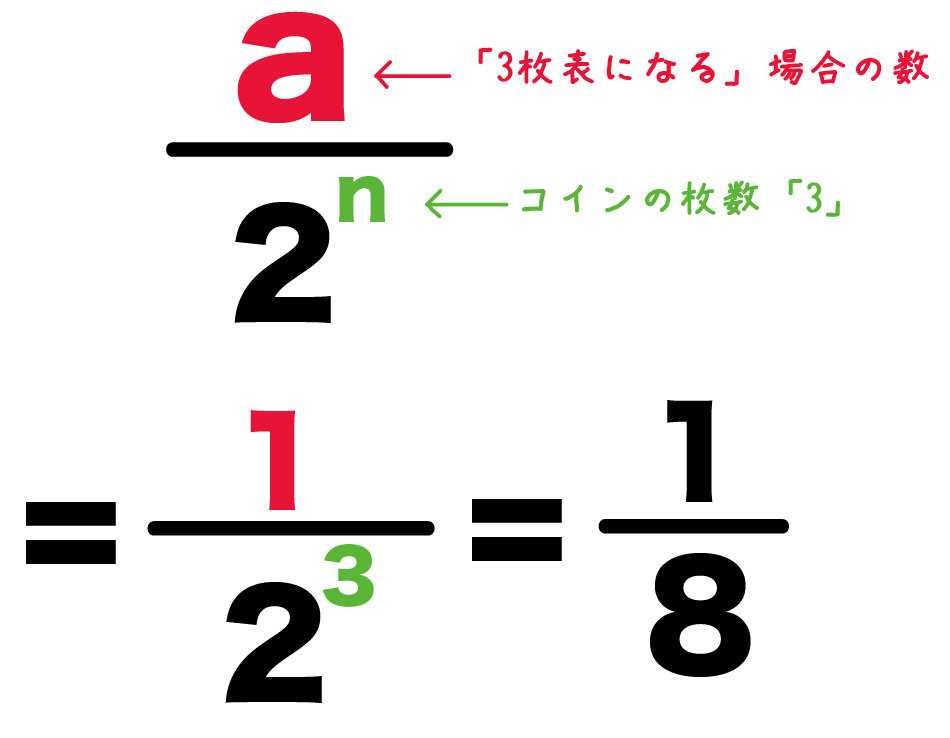



簡単公式 コインの確率を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
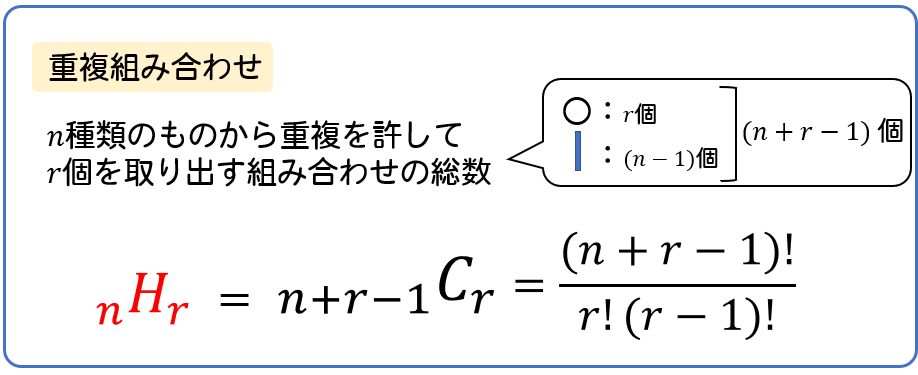



重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ
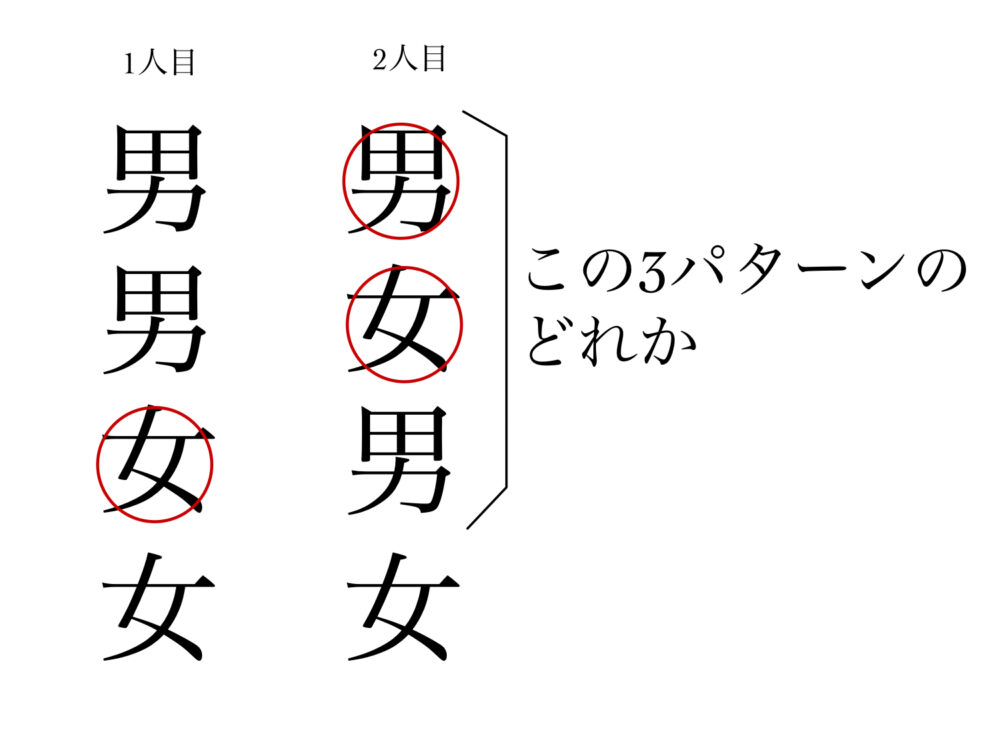



条件付き確率の公式や求め方とは 問題を使ってわかりやすく解説 東大医学部生の相談室
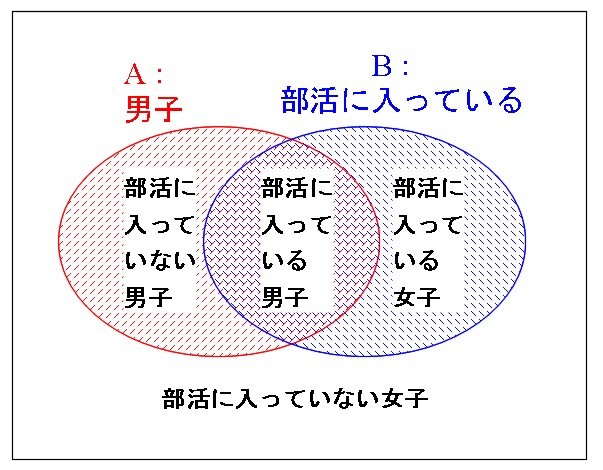



条件付き確率の公式を使う問題と公式を使わない計算の方法




じゃんけんの確率問題 考え方を徹底解説 あいこになるときは じゃんけんが2回のときは 全部解説します ますますmathが好きになる 魔法の数学ノート



V 0uat1ct0ao8m



反復試行の確率 独立試行の確率とは 公式や見分け方 受験辞典




条件付き確率についてなんですが 写真の公式のpa B とn Aかつb の違いがわかり Clear




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




数学1a 場合の数を解説 公式を使って入試問題を解いてみよう Himokuri
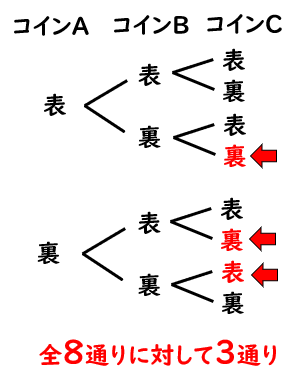



中学数学の確率の問題の解き方 コイン サイコロ くじ カード 数学fun




反復試行の確率の公式 なぜ組合せcが出てくる 応用問題4選も解説 遊ぶ数学




受験 定期試験 数学解き方集 裏技 解法 確率応用 高校数学
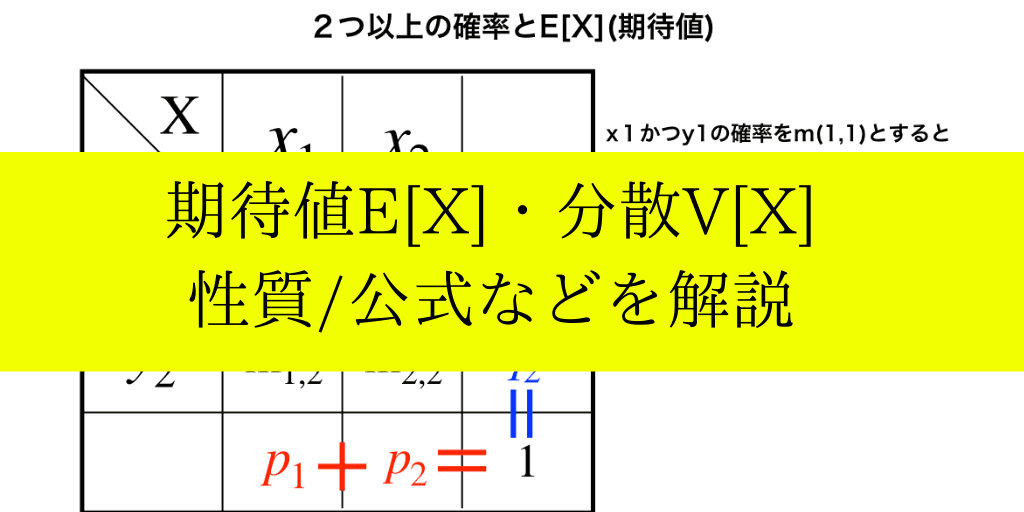



期待値e X と分散v X の性質や計算ルール 同時確率分布のまとめ



条件付き確率



同時確率 条件付き確率とは 制御工学の基礎あれこれ




確率分布 分散の計算公式の使い方 数学b 定期テスト対策サイト




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ




受験 定期試験 数学解き方集 裏技 解法 じゃんけん 中学 高校



条件付き確率とはサイコロやベン図でわかりやすく 公式の読み方は いちばんやさしい 医療統計




場合の数と確率 の公式集 高校数学なんちな
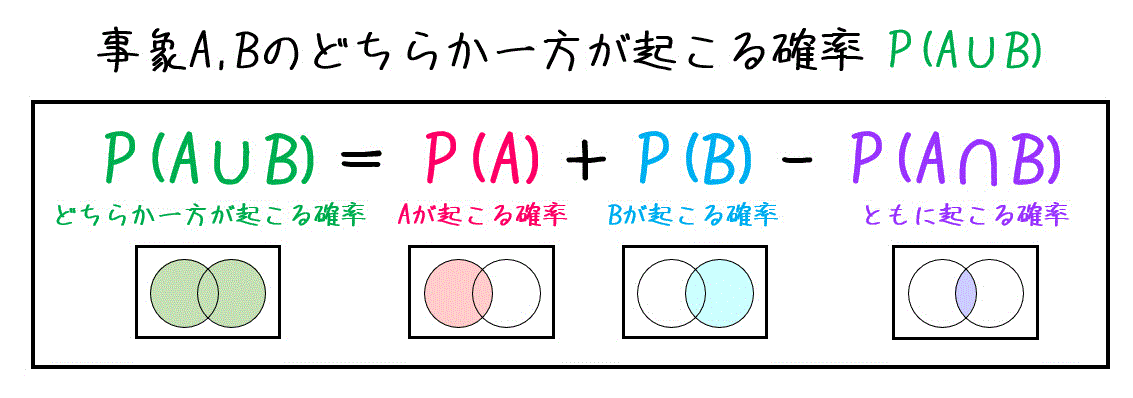



確率 1時間でマスター 覚えておくべき5つの法則 公式 工業大学生ももやまのうさぎ塾




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ




確率9 反復試行の公式はない方がよい 怜悧玲瓏 高校数学を天空から俯瞰する




数aの条件付き確率で 写真の公式を使うときの違いを教えてほしいです Clear
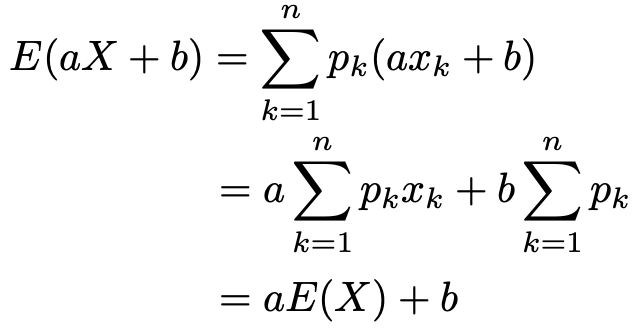



離散型確率変数の期待値と分散 中学の数学からはじめる統計検定2級講座第4回 とけたろうブログ




条件付き確率の公式とは 不良品の問題など4選もわかりやすく解説します 遊ぶ数学




確率10 反復試行の公式はない方がよい2 怜悧玲瓏 高校数学を天空から俯瞰する




中学数学 確率 二つのサイコロが出てくる確率の問題を攻略 Youtube




条件付き確率 丸暗記ダメ 絶対 オモワカ マジさえ確率 13 数学専門塾met Note



確率 1時間でマスター 覚えておくべき5つの法則 公式 工業大学生ももやまのうさぎ塾




確率公式3 大学受験の王道
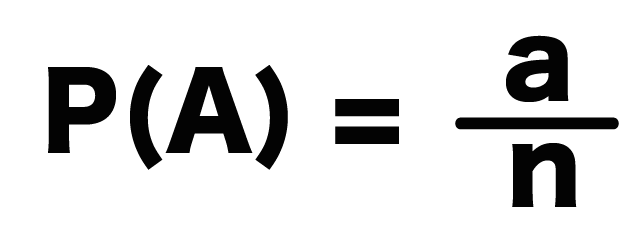



中学数学 確率の求め方がわかる1つの公式 計算式 Qikeru 学びを楽しくわかりやすく




条件付き確率の基本 合格タクティクス




高校数学a じゃんけんの確率 N人のじゃんけん 受験の月



条件付き確率 ベイズの定理 ベイズの展開公式 ベイズ更新 Ppt Download



確率とは 公式 問題での計算式の立て方と解き方 受験辞典



2 は 条件付き確率の公式を覚えて解くしかないですか 公式を使わず Yahoo 知恵袋




数学b編 完全攻略 高校数学の公式全部まとめてみたwww Cupuasu クプアス




数a 確率 写真の 1 が分かりません Clear




条件付き確率の公式と求め方を分かりやすく解説




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ




5分で分かる 確率統計 Ncr の計算方法 あぱーブログ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



条件付き確率とは 公式や問題 ベイズの定理 不良品の例 も 受験辞典




確率公式2 大学受験の王道




確率変数の和の期待値の求め方と公式 高校数学b Youtube
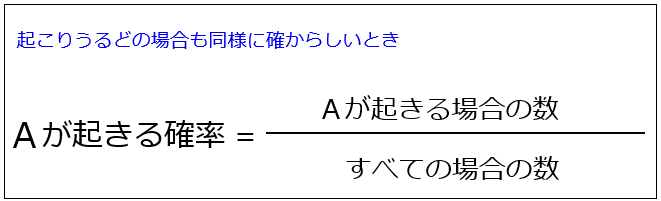



確率計算の公式から 確率の求め方の苦手ポイント 同様に確からしい を武器に変える記事 アタリマエ




5分で分かる 確率統計 Ncr の計算方法 あぱーブログ




場合の数と確率 条件つき確率の解き方について 数学a 定期テスト対策サイト




高校数学a 順列 の確率1 基本 例題編 映像授業のtry It トライイット




確率 1時間でマスター 覚えておくべき5つの法則 公式 工業大学生ももやまのうさぎ塾




17年準確率達98 的殺二碼公式 年度鉅獻 在準確率中笑看主任 雪花新闻



全確率の公式



確率の問題です この問題自分は反復試行の公式で解いてないんで Yahoo 知恵袋




ファイナンスのための確率微分方程式 ブラック ショールズ公式入門 Amazon Com Books




反復試行の確率の公式といろいろな例題 高校数学の美しい物語



0 件のコメント:
コメントを投稿